Phương pháp kiểm định sự phù hợp của hàm hồi quy được sử dụng nhiều trong dự báo kinh tế. Kết quả phân tích dùng để ước lượng và dự đoán giá trị trung bình của một biến trên số liệu đã biết của biến khác. Hãy cùng chúng tôi tìm hiểu rõ hơn về hàm hồi quy này ở bài viết dưới đây nhé!
Phân tích hồi quy nhằm đạt được kết quả ước lượng tốt nhất về mối quan hệ chân thực giữa các biến số trong kinh tế lượng .
Tổng hợp các thông tin về hàm hồi quy
Hàm hồi quy là gì?
Hàm hồi quy là tập hợp tất cả các cá thể hay các nhân tố có cùng một hoặc vài đặc tính chung.
Kiểm định sự phù hợp của hàm hồi quy là một phương pháp thống kê mà giá trị kỳ vọng của một hoặc nhiều biến ngẫu nhiên được dự đoán dựa trên điều kiện của các biến ngẫu nhiên (đã tính toán) khác. Cụ thể gồm có hồi quy tuyến tính, hồi quy Poisson, hồi quy lôgic và học có giám sát. Để hiểu rõ hơn về các cách kiểm định cũng như đánh giá mức độ phù hợp của hàm hồi quy trong kinh tế lượng, mời bạn tham khảo bài viết dưới đây!
Ví dụ: tập hợp tất cả người Việt nam đang theo học tại các trường trung cấp, cao đẳng và đại học là tổng thể sinh viên của Việt Nam.
Phân tích hồi quy là gì?
Phân tích hồi quy (regression analysis) là kỹ thuật thống kê dùng để ước lượng xem phương trình phù hợp nhất với các tập hợp kết quả quan sát giữa biến phụ thuộc và biến độc lập. Nó cho phép đạt được kết quả ước lượng tốt nhất cho mối quan hệ chân thực giữa các biến số. Từ phương trình ước lượng này, người ta có thể dự báo về biến phụ thuộc (chưa biết) dựa trên giá trị cho trước của biến độc lập (đã biết). Phân tích hồi quy quan tâm đến mối liên hệ của biến phụ thuộc với một hay nhiều biến giải thích (biến độc lập) qua việc ước lượng hoặc dự đoán giá trị trung bình của tổng thể.
Cách kiểm định sự phù hợp của hàm hồi quy
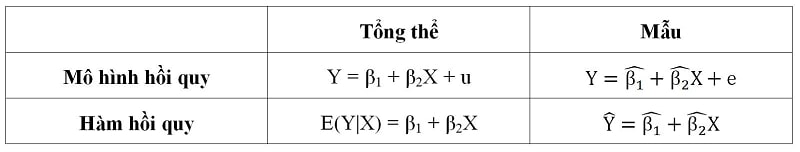
Phân tích hồi quy không chỉ trùng khớp đường cong (lựa chọn một đường cong mà vừa khớp nhất với một tập hợp điểm dữ liệu). Nó còn trùng khớp với một mô hình với các thành phần ngẫu nhiên và xác định (deterministic and stochastic components). Trong đó thành phần xác định gọi là bộ dự đoán (predictor) và thành phần ngẫu nhiên gọi là phần sai số (error term).
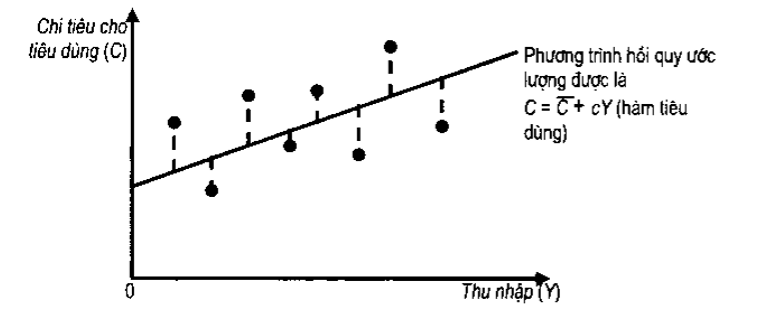
Hình trên biểu thị tập hợp các kết quả quan sát dưới dạng đồ thị và chúng ta phải tìm phương trình của đường thẳng đó dựa trên điều kiện nó phù hợp nhất với số lượng thu thập được, vì một đường phù hợp sẽ mang lại kết quả dự báo tốt nhất cho biến phụ thuộc. Đường thẳng phù hợp nhất với số liệu bắt buộc phải lựa chọn sao cho giá trị tổng bình phương các độ lệch (khoảng cách) theo phương thẳng đứng giữa các điểm và đường thẳng đạt nhỏ nhất. Phương pháp bình phương nhỏ nhất thông thường này sẽ được ứng dụng hầu hết các phân tích hồi quy. Tính phù hợp của đường hồi quy với những kết quả quan sát mẫu sẽ phản ánh bằng hệ số tương quan.
Chúng ta có thể xác định các biến mục tiêu và biến độc lập có quan hệ với nhau hay không cũng như có quan hệ như thế nào về mặt định lượng chỉ qua phương pháp hồi quy. Tuy nhiên, trong những trường hợp muốn tìm hiểu nhanh chóng 2 biến bất kỳ có quan hệ với nhau, mức độ quan hệ ra sao nhưng chưa cần dùng đến phương pháp hồi quy phức tạp hoặc muốn kiểm chứng từ phương trình hồi quy lần nữa xem 2 biến có quan hệ với nhau hay không, thì phương pháp phân tích tương quan sẽ cho chúng ta kết quả nhanh chóng.
Phương trình hồi quy không mang lại dự báo chính xác về biến phụ thuộc khi biết giá trị của các biến độc lập. Bởi các hệ số hồi quy ước lượng từ kết quả quan sát mẫu chỉ là con số ước lượng tốt nhất cho các tham số chân thực từ tổng thể, vì vậy chúng phụ thuộc vào các biến thiên ngẫu nhiên. Để xác nhận tính chất không hoàn hảo của tất cả những phương trình hồi quy ước lượng dựa trên một mẫu xác định mối quan hệ chân thực trong tổng thể, phương trình hồi quy thường được viết như sau:
C = C¯ + cYd + e
Kiểm định sự phù hợp của hàm hồi quy hai biến
Đầu tiên, ta thực hiện phương pháp kiểm định giả thiết dựa trên các thông tin như sau:
- Ho:R2 = 0
- H1:R2≠ 0
- Với độ tin cậy là: 1- α.
Sau đó, ta thực hiện phương pháp kiểm định F thông qua các bước như sau:
Bước 1: Tính
Bước 2: Tra bảng tìm F(1, n-2) với mức ý nghĩa là α.
Bước 3: Nếu F>F(1, n-2) thì bác bỏ H0.
Nếu F≤F(1, n-2) thì chấp nhận H0.
Trên đây là các thông tin nhằm giúp các bạn kiểm định sự phù hợp của hàm hồi quy trong kinh tế lượng, giúp chúng ta nhận được phương trình phù hợp nhất. Hy vọng các thông tin trên đây sẽ cung cấp đến bạn những kiến thức hữu ích nhất.

